Солитоны, бризеры и локализованные вихри в гидродинамике

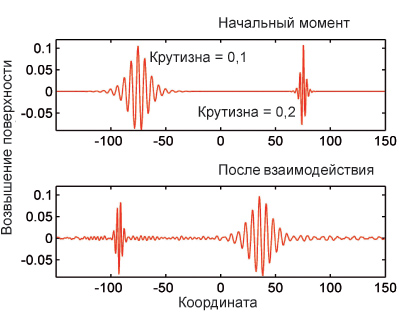
Еще один классический объект нелинейной физики – уединенные волны (солитоны). Их эволюция и взаимодействие играют определяющую роль в развитии нелинейной стадии самых разнообразных волновых возмущений. Одним из наиболее интересных и наглядных примеров являются солитоны большой амплитуды в неинтегрируемых гидродинамических системах. Важным результатом в этом направлении стало установление полной аналогии между взаимодействием солитонов и столкновением классических частиц.

Развитый в ИПФ универсальный подход к описанию динамики ансамблей солитонов как частиц дал возможность классифицировать различные типы взаимодействия уединенных волн по критерию «притяжение – отталкивание», сформулировать необходимые условия существования связанных состояний солитонов (мультисолитонов) и получить общие представления о возможных типах движений в бесконечных цепочках солитонов (К. А. Горшков, Л. А. Островский, И. А. Соустова).

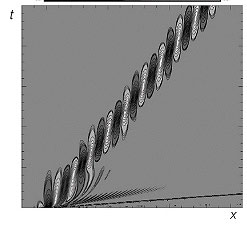
Новые классы локализованных осциллирующих волновых пакетов большой амплитуды (бризеров или солитонов огибающих) исследованы в многослойных гидродинамических потоках; они существуют на временах, значительно превышающих характерный период пакета. Найденные в численных расчетах солитоны огибающих большой амплитуды на поверхности глубокого моря являются сейчас прообразами волн-убийц, неожиданно возникающих на поверхности океана; эти пакеты, как и солитоны, взаимодействуют без потери своей идентичности (Е. Н. Пелиновский, А. В. Сергеева, А. В. Слюняев, Т. Г. Талипова).

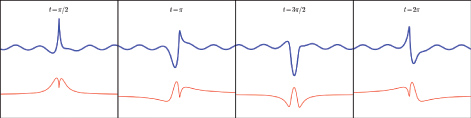
Аналогичное поведение обнаруживают локализованные вихревые образования на поверхности жидкости, так называемые волны Герстнера (А. А. Абрашкин). На рисунке ясно видна эволюция бризерного возмущения на фоне однородного волнения.

Другие важные результаты, полученные в ИПФ при изучении вихревых течений, связаны с использованием подхода Лагранжа к гидродинамике идеальной жидкости. С помощью лагранжевых переменных найден новый класс точных решений уравнений гидродинамики, описывающий нестационарные, неоднородно завихренные, плоские течения, в которых отдельные жидкие частицы движутся по эпициклоидам или гипоциклоидам (получившим название птолемеевских течений). Предложены описание динамики одиночной вихревой области в окружающем потенциальном течении (птолемеевский вихрь), обобщающее классическое решение для вихря Кирхгофа, а также матричная формулировка уравнений гидродинамики идеальной жидкости в форме Лагранжа, на основе которой построено пространственное обобщение класса птолемеевских течений. Движение частиц жидкости в таких потоках является суммой трех круговых вращений с различными амплитудами, частотами и пространственной ориентацией (А. А. Абрашкин, Д. А. Зенькович, Е. И. Якубович).

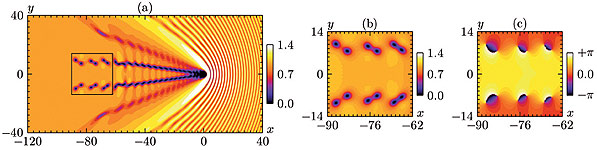
В последнее время теория солитонов и вихрей нашла приложение в быстроразвивающейся области нелинейной атомной физики, связанной с исследованием когерентных волн материи, причем удается наблюдать квантовые эффекты на макроскопических масштабах. В ИПФ проведено исследование кильватерного следа за препятствиями, движущимися в однородном бозе-эйнштейновском конденсате (В. А. Миронов, Л. А. Смирнов).

Получены следующие результаты:

• Для дозвукового режима движения барьера характерно наличие критической скорости (соответствующей критерию Ландау в теории сверхтекучести), при превышении которой ламинарное (чисто потенциальное) течение становится неустойчивым. При этом за препятствием начинают парами возбуждаться вихри с различными по знаку топологическими зарядами. Эти вихревые пары взаимодействуют друг с другом с излучением звуковых волн, и происходит турбулизация кильватерного следа.
• За сверхзвуковыми барьерами малой интенсивности внутри конуса Маха имеется область тени. Сильно возмущающие сверхзвуковые барьеры оставляют за собой кильватерный след из четного числа квазиодномерных провалов концентрации (темных солитонов), лежащих внутри конуса Маха. Из-за развития модуляционной неустойчивости кильватерный след эволюционирует в вихревую дорожку типа дорожки Кармана.
• На основе асимптотической процедуры аналитически показано как слияние пары «вихрь – антивихрь» в процессе движения в области более плотной среды, так и образование солитона типа Кадомцева – Петвиашвили.