Самовоздействие, градиентная катастрофа, волновой коллапс

Эффекты самовоздействия волновых пакетов и пучков в нелинейных средах привлекли широкое внимание исследователей еще в 1960-х годах в связи с появлением лазеров и быстрым развитием нелинейной оптики, и к настоящему времени эта тематика стала уже классическим направлением в области нелинейной физики. Ряд важнейших результатов принадлежит сотрудникам ИПФ (А. Г. Литвак, В. А. Миронов, А. М. Сергеев, В. И. Таланов, Г. М. Фрайман).

Разработана общая теория явлений самовоздействия волн в средах с различными механизмами нелинейности, на ее основе изучен широкий круг эффектов самофокусировки и самомодуляции электромагнитных волн в диэлектриках, жидкостях, газах и плазме, в том числе:

• развита теория стационарной и нестационарной самофокусировки волновых пучков;
• открыты явления филаментационной и модуляционной неустойчивости волн, и построена теория нелинейной стадии этих процессов;
• исследовано подавление филаментационной неустойчивости при самовоздействии в средах с инерционной нелинейностью;
• исследована нелинейная динамика сверхкоротких лазерных импульсов в диспергирующих средах;
• изучены бризеры большой амплитуды, возникающие в результате модуляционной неустойчивости, применительно к проблеме волн-убийц в нелинейных диспергирующих системах;
• исследованы пространственно-временные коллапсы трехмерных волновых пакетов.

Эти результаты широко применяются при разработке мощных лазерных систем и установок по нагреву плазмы, методов создания сверхкоротких оптических импульсов, методов прецизионных оптических измерений констант нелинейности различных сред и кривизны волновых фронтов оптических пучков, при построении прогностических моделей эволюции интенсивных внутренних волн на океаническом шельфе и объяснении феномена волн-убийц.

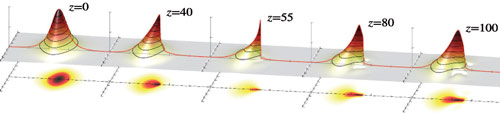
Развитие оптических методов генерации аттосекундных и терагерцовых импульсов поставило проблему теоретического исследования динамики самовоздействия волновых полей с шириной спектра порядка несущей частоты. В ИПФ РАН (А. Г. Литвак, В. А. Миронов, А. А. Балакин, С. А. Скобелев) развит подход к исследованию таких волн, основанный на использовании уравнений Максвелла в безотражательном приближении. В частности, методом моментов найдено достаточное условие коллапса в системе. Использование преобразования автомодельного типа показало, что ключевым процессом в динамике системы является укручение продольного профиля импульса. Удалось доказать, что этот процесс несколько опережает самофокусировку поля. В результате происходит образование более сложной особенности поля, в которой градиентная катастрофа сопровождается коллапсом.