Microscopic theory of the second-order phase transitions and critical phenomena
Despite the applied orientation of the Institute, great attention in its work is given to the solution of the fundamental problems in the theoretical physics. Recently, the long-standing problem of finding the microscopic theory and universal mechanism of the second-order phase transitions has been solved. The basics of the non-perturbation microscopic theory of the spontaneous symmetry breaking and related critical phenomena have also been formulated. The theory is based on the explicit isolation of the universal constraint nonlinearity (interaction), which is determined by the breaking symmetry and originates due to restraining the many-body Hilbert space by the integrals of motion (constraints) in accordance with the Noether theorem. That constraint-cutoff mechanism is responsible for the phase transition to the state with the Bose-Einstein condensate even in an ideal gas, i.e., in the absence of the inter-particle interaction (V. V. Kocharovsky, Vl. V. Kocharovsky).
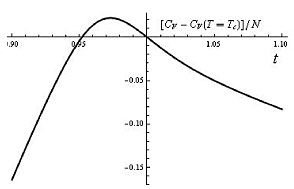
The universal probability distribution of the number of particles in the Bose-Einstein condensate of an ideal gas in a mesoscopic trap with arbitrary temperature, volume, and particle number has been found and described by the exact analytical formula for the first time. All universality classes and a remarkable self-similarity of the statistics and thermodynamics of the Bose-Einstein condensed ideal gas in different mesoscopic traps have been found. In particular, a universal critical behavior of the specific heat capacity in the critical region, i.e., a universal structure of the lambda point, has been found analytically for an ideal gas in a mesoscopic trap. It has been shown that the obtained universal formulas for the order parameter and all higher moments of the condensate fluctuations match the known asymptotics on both sides of the critical region (the Landau mean-field theory) and agree with the specific results of the phenomenological renormalization-group theory, which is valid in the narrow central part of the critical region.